ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
Define trigonometric ratios and solve problems involving right triangles Videos 5 videos
Sine is the opposite over the hypotenuse; cosine is the adjacent over the hypotenuse; and tangent is the opposite side over the adjacent side....
FYI: cats don't like to get wet. Okay, so that fact won't be relevant every time you solve trig equations, but it happens to be this time.
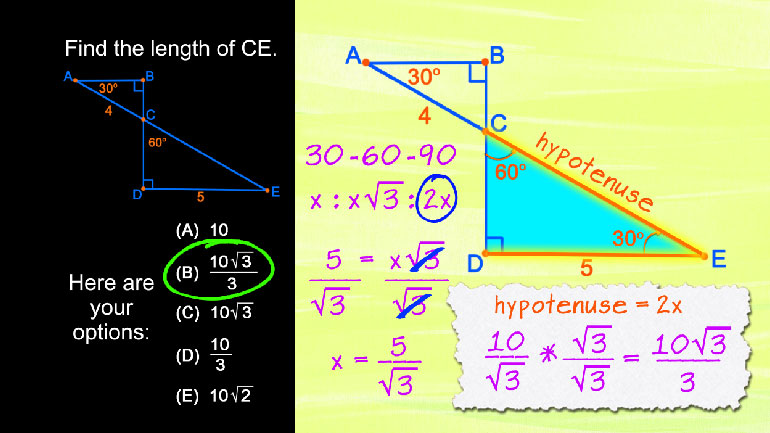
SAT Math 1.3 Geometry and Measurement. Find the length of CE.
Special Right Triangles 1976 Views
Share It!
Transcript
- 00:05
Right and Special Right Triangles, a la Shmoop. Put down your chainsaws...
- 00:12
...because the annual Lumberjack Ball is tonight! Unfortunately, Lumberjack Bill, the one who
- 00:17
can never get a date...
- 00:19
...decided to steal the lumberjack dancin' square the night before...
- 00:22
...leaving the poor lumberjacks to rebuild the whole thing before tonight's ball.
Full Transcript
- 00:26
Here's what the square looked like last night.
- 00:34
The lumberjack waltz requires there to be a distance of 4 between point B and point
- 00:39
D.
- 00:40
Knowing length B prime D prime is 4, what is the length of a side of the square ABCD?
- 00:47
Here are your choices: Well, to start, it helps to know that squares
- 00:53
have four right angles and four equal sides.
- 00:59
Since angle D is in the corner of square ABCD, we know it's a 90 degree angle.
- 01:05
Zoom in on triangle B prime D D prime. We know it's a right triangle, so we can use
- 01:12
the Pythagorean theorem to solve it.
- 01:14
We know its hypotenuse, but not its two side lengths.
- 01:18
Whatever will the lumberjacks do?
- 01:20
Since A prime B prime C prime D prime is also a square, we know that angle D prime is also
- 01:27
90 degrees.
- 01:29
Angle D D prime C is a straight angle, so it has a measure of 180 degrees.
- 01:34
Subtract 90 degrees for angle B prime D prime C prime, and we only have 90 degrees to share
- 01:41
among the two smaller side angles.
- 01:43
Splitting them up evenly, each angle gets 45 degrees.
- 01:47
If we do that with all the angles, we'll see that our triangle B prime D D prime is a special
- 01:52
right triangle, a 45-45-90 triangle.
- 01:57
Since both its acute angles are congruent, we know the lengths of its legs are congruent.
- 02:03
Good thing, too; otherwise square dancing would be a big mistake.
- 02:07
Now we can use the Pythagorean theorem and replace both a and b with the same length:
- 02:14
x.
- 02:16
That's the wonderful thing about 45-45-90 triangles. If the length of the leg is x,
- 02:28
the hypotenuse will always be equal to x times the square root of 2.
- 02:34
We're looking for the side of the big square, ABCD.
- 02:38
If we look at the picture, we know that D prime D is the same length as D prime C, so
- 02:43
we just have to multiply 2 root 2 by 2. That gives us 4 root 2.
- 02:50
So, long story short... if it isn't already too late... our answer is D.
- 02:57
Now those lumberjacks can rebuild their perfect square and get ready to dance.
- 03:01
Swing your chainsaw 'round and 'round!
Related Videos
Haven't you always wondered how much cardboard it takes to encase a trunk warmer for your pet elephant?
Want to figure out the area and perimeter of irregular shapes? Break them down into regular shapes. For example, a flower can be broken down into s...
It's one thing when all those shapes are sitting flat on the page. But when they start popping out and invading our personal space bubble, we get a...
Does thinking about 3D Geometry get you bent out of shape? Never fear! Watch this video and figure out some fun new shapes to bend back into. We're...
ACT Math: Plane Geometry Drill 3, Problem 5. How long would it take for the wheel to make two rotations?