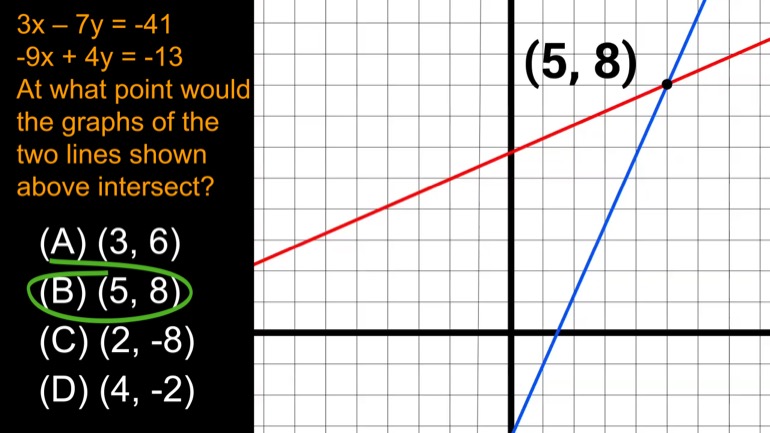
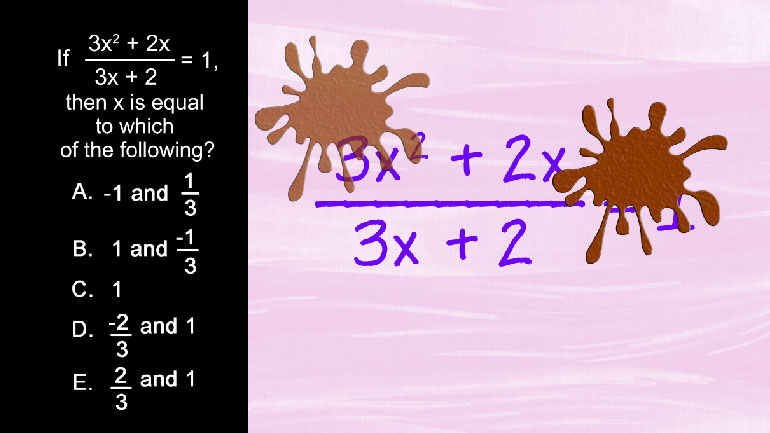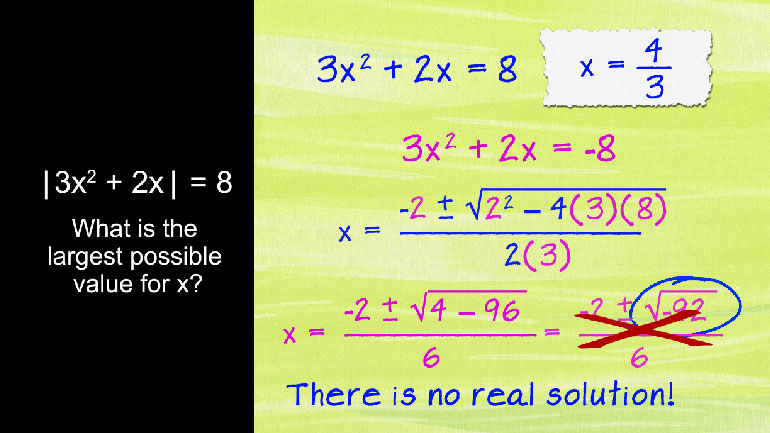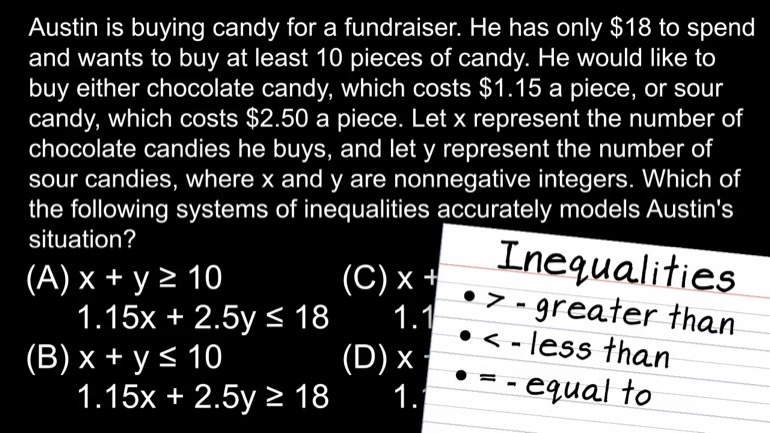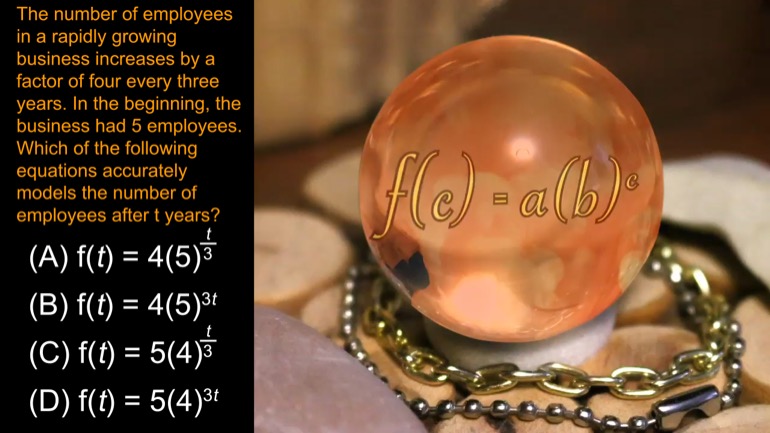ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
Algebra and Functions Videos 140 videos
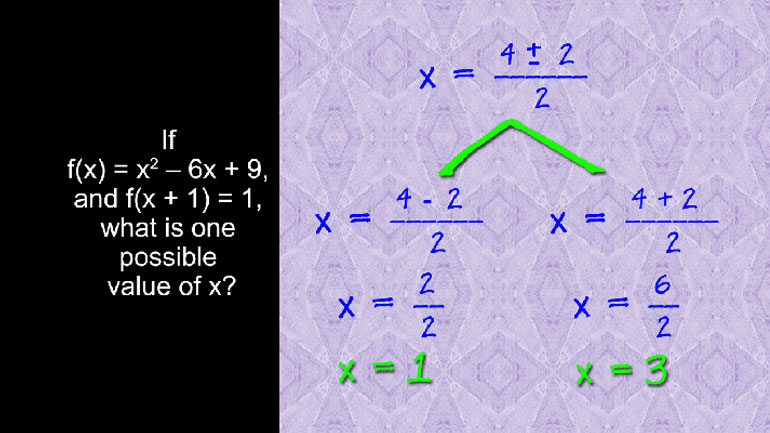
SAT Math: Algebra and Functions Drill 1, Problem 2. Based on the data in the table, what is the maximum heart rate for the average 22-year-old?
SAT Math 1.3 Algebra and Functions. How many 16 oz. bottles did she buy?
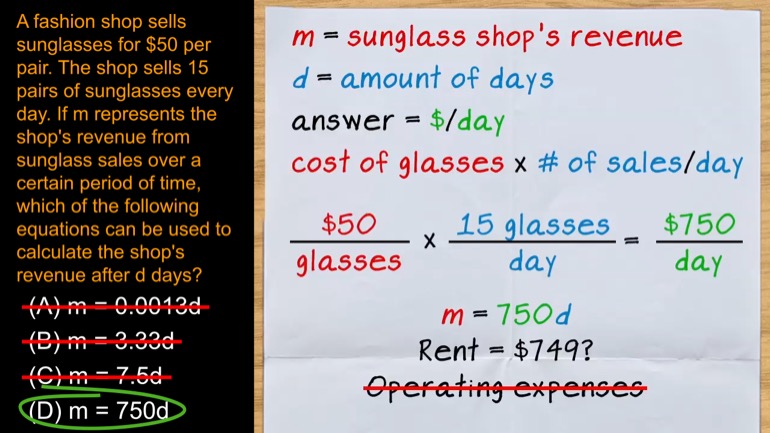
SAT Math: Which Equation Models a Company's Exponential Growth? 3 Views
Share It!
Description:
The number of employees in a rapidly growing business increases by a factor of four every three years. In the beginning, the business had 5 employees. Which of the following equations accurately models the number of employees after t years?
Transcript
- 00:03
Okay Shh Mash bumpers Another word problem coming at us
- 00:07
The number of employees and a rapidly growing business increases
- 00:10
by a factor of four every three years That is
- 00:14
they go from like one hundred four hundred three years
- 00:17
In the beginning the business had five employees which of
Full Transcript
- 00:20
the following equations accurately models the number of employees after
- 00:24
t years All right so what we're looking at these
- 00:31
they got four times five two done five times for
- 00:34
so we got to think through this little bit carefully
- 00:35
for a company to grow this fast they'd have to
- 00:38
be super successful smart and good looking We're not saying
- 00:42
this mystery company is from up at all We're just
- 00:44
saying that we're super successful smart and good looking Not
- 00:48
really Well some people might say this company just has
- 00:51
lots and lots of luck but we can make an
- 00:53
equation to predict their luck It's an algorithmic one that
- 00:57
revolves around search here That was a better hit for
- 01:00
the company we're talking about Well the equation for exponential
- 01:02
growth will be helpful here in this equation A is
- 01:05
the initial amount b is the growth factor per unit
- 01:08
time that see years t and sees how much time
- 01:12
has passed or how many years has passed So if
- 01:14
you didn't get this equation well a good luck it's
- 01:17
could be a hard hard question to answer So f
- 01:20
c equals a times quantity b to the sea on
- 01:23
ly two answers have five in the right place Like
- 01:26
where a is that a c and d right there
- 01:28
The hard part is seeing what c should be Well
- 01:31
it takes three years for the number of employees to
- 01:33
grow four times larger than it was before so at
- 01:37
t equals zero We should have the initial amount five
- 01:41
employees then at t equals three We should have five
- 01:45
times four twenty employees and then five times the quantity
- 01:50
for square and that eighty like five times sixteen employees
- 01:54
at equal six So using the fraction t over three
- 01:57
for sea giving us fft equals five times quantity for
- 02:01
two the third there So the answer is c and 00:02:05.557 --> [endTime] wow this pretty hard problem that we're done
Related Videos
In the equation above, if a, b, and c are all constants, what is c?
When x = 12, a certain polynomial, y, equals 0. Which of the following must be true about the polynomial y?
SAT Math 1.1 Algebra and Functions. Find an algebraic equation to correspond with the data.
SAT Math 1.1 Geometry and Measurement. What is the circumference of the circle?
SAT Math 1.1 Numbers and Operations. How many combinations of beverage and cereal can be made?