Answer
One way is to think of the function as
f(x) = (x3sin x)cos x.
In this case,
f ' (x) = (x3sin x)'cos x + (x3sin x)(cos x)'.
We need to use the product rule again to find one of the derivatives we need:
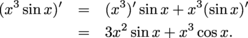
Now we put this back into the product rule:
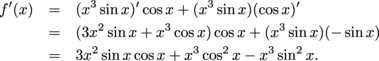
The other way is to think of the function as
f(x) = (x3)(sin x cos x).
In this case, we'll need to use the product rule to find
(sin x cos x)'
before we can find the derivative of the original function. Here we go:
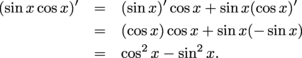
While cos2x + sin2x = 1, cos2x – sin2x isn't anything in particular; we can't make this any nicer.Now we can use the product rule to find f'.
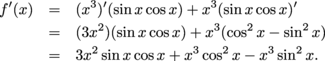
Thankfully, we found the same answer either way.