ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
Quadratic Equations Videos 11 videos
GED Math: Expression and Equations Drill 3, Problem 4. What are the roots of the quadratic equation?
GED Math: Expression and Equations Drill 4, Problem 2. Which of the following inequalities should Jabari solve in order to determine the values of...
The discriminant is part of the quadratic formula, but that doesn't mean it isn't important in its own right; in fact, once it even guest-hosted Th...
SAT Math 9.5 Algebra and Functions 213 Views
Share It!
Description:
SAT Math 9.5 Algebra and Functions
Transcript
- 00:02
Here's a question that's part of a balanced Shmoopy breakfast.
- 00:06
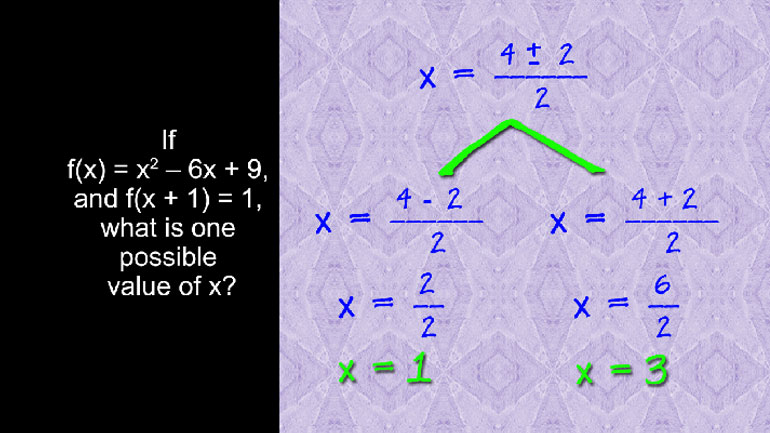
If f (x) = x squared – 6x + 9, and f (x + 1) = 1, what is one possible value of x?
- 00:16
Well, it wants us to find one possible value of x, which just means… solve for x.
- 00:21
The requirements for a value of x are: f of x is equal to x squared - 6x + 9, and f of x + 1 = 1.
- 00:31
We’ll need to put together the two requirements to find x.
Full Transcript
- 00:37
Let’s take a closer look at the second requirement.
- 00:40
This just means that if we plugged the value (x + 1) into the function,
- 00:44
which we’re given in the first requirement, we can solve for x.
- 00:47
To solve this equation, we’re first going to have to turn it back into a polynomial.
- 00:51
So, we expand (x + 1) squared first.
- 00:55
By applying foil, we turn (x + 1) squared into x squared + 2x + 1.
- 01:03
Then, we distribute -6 into the second parentheses. We get -6x - 6.
- 01:10
Now we can combine like terms. There’s only one x squared term, so that stays by itself.
- 01:15
However, we have both 2x and -6x, so we can combine those to -4x.
- 01:20
Then, all of the constants add to +3. Great, we have a polynomial!
- 01:24
To be more specific… it's a quadratic.
- 01:27
We can just stick this puppy into the quadratic formula and come out with the answer.
- 01:31
Plugging in our values, we get that x is equal to 4 plus or minus the square root of 16 – 12 over 2.
- 01:40
This simplifies to 4 plus or minus 2 over 2. The possibilities are 1 or 3.
- 01:47
That's our answer either 1 or 3.
Related Videos
SAT Math 2.1 Geometry and Measurement. What is the measure of angle z in terms of x and y?
In 2014, the unemployment rate of one county in California was 7%. In another county, the unemployment rate was 11%. Which of the following express...
Angela is making cookies for a bake sale. She expects each batch of her cookies to sell for $40. It costs her $10 to make one batch of cookies, and...