ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
Implementing algebraic/computational processes Videos 5 videos
AP Calculus 1.1 Applications and Multivariable Calculus. Which of the following is a direction field for the differential equation?
What do snickerdoodles and velocity have in common? Derivatives! No, that wasn't a bad attempt at a joke. Get on our level by watching this speedy...
AP Calculus AB/BC 1.5 Limits 265 Views
Share It!
Description:
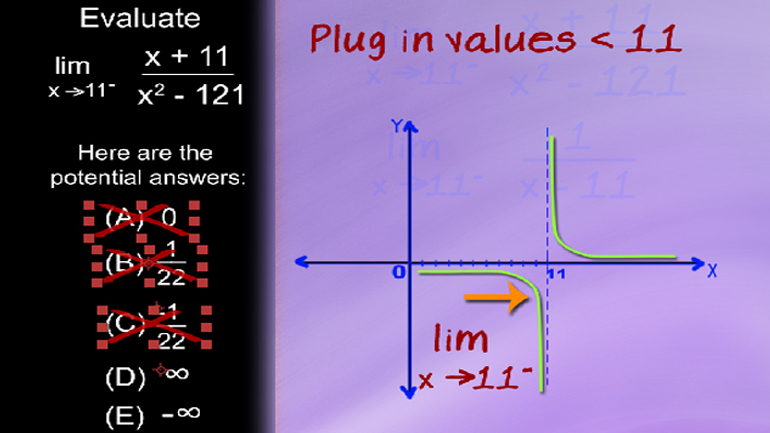
AP Calculus: AB/BC Limits Drill 1, Problem 5. Evaluate the limit.
Transcript
- 00:03
Here's your shmoop du jour: Evaluate the limit as x approaches 11 from
- 00:08
the negative side of x plus 11 over x squared minus 121.
- 00:13
Here are the potential answers...
- 00:18
Whenever we're given a limit problem like this and asked to evaluate it, the first thing
- 00:22
we can do is just try plugging in 11 directly.
Full Transcript
- 00:25
On the top of the fraction, 11 plus 11 works out as 22...
- 00:29
...but when we plug it in to the denominator, we get that 11 squared is 121
- 00:34
and 121 minus 121 is 0.
- 00:39
Dividing by zero is a big no-no. You can't do that!
- 00:43
So to avoid that situation, let's try simplifying the bottom.
- 00:46
x squared minus 121 looks like a difference of two squares...
- 00:50
...a squared minus b squared equals a plus b times a minus b.
- 00:56
The square root of 121 is 11. So applying the formula, the bottom simplifies to x plus
- 01:01
11 times x minus 11.
- 01:03
The x plus 11 on the top and bottom of the fraction cancel out... and we're left with the
- 01:08
limit as x approaches 11 from the negative side of 1 over x minus 11.
- 01:14
Back to the question...it asks us to take the limit as x approaches 11 from the negative side.
- 01:20
Whenever we deal with limits, it means we get really close to a number from the negative
- 01:24
side but never actually kiss it.
- 01:26
If we try plugging in 11 as x again...11 minus 11 still gives us 0 in the denominator...
- 01:33
...so we can immediately eliminate (A), (B), and (C) because this function is not defined.
- 01:37
So we're left with D) or (E). We can now start plugging in values smaller
- 01:42
than 11 that get closer and closer to 11...since we're approaching 11 from the negative side.
- 01:47
If x equals 10, we get 1 over 10 minus 11, or negative 1.
- 01:52
If x equals 10.5... then 1 over negative .5 gives us
- 01:57
an even larger negative number...or negative 2.
- 02:00
Looks like we're getting more and more negative....and will keep approaching negative infinity...
- 02:06
So our answer is (E). Done!
Related Videos
AP Calculus: Problem Explanation Limits Drill 1, Problem 1. Which of the following are true about the pictured function?
If you're working on developing a positive self-image, don't ever weigh yourself on planet Deneb-G73. Either the gravitational pull there is a tad...
Breathe in deeply through the nose... Now slowly exhale... Breathe in... And out... Now visualize the graph of the limit of f(x) as x approaches 2....
AP Calculus 1.4 Limits. Given the limit, which of the following are true?
AP Calculus 2.3 Limits. Which of the following facts is helpful in determining the limit?