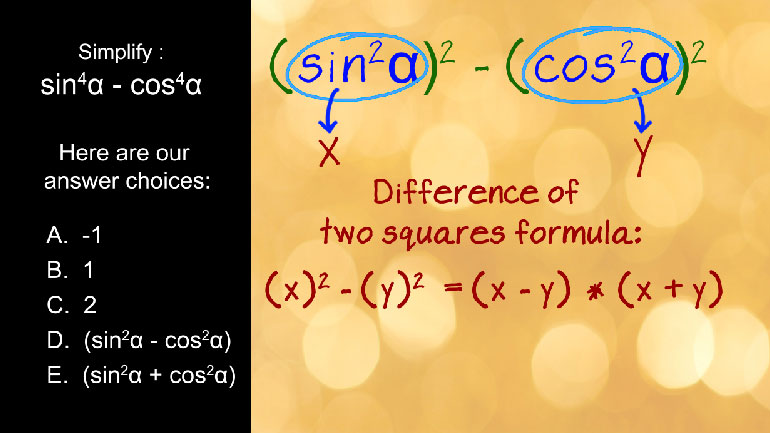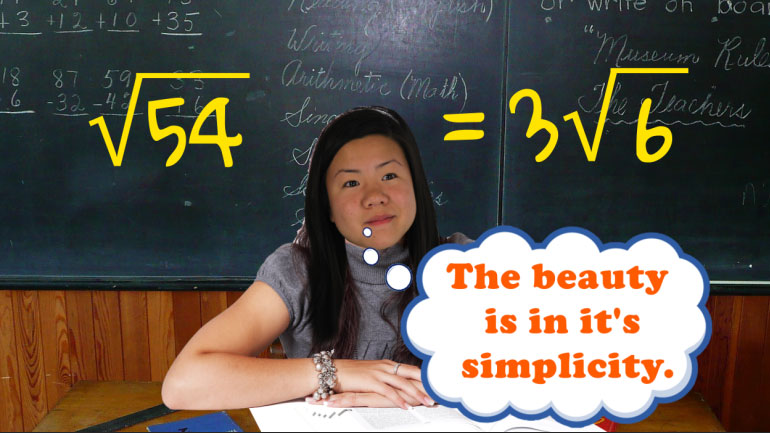ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
Product Type Videos 3763 videos
ACT Math: Trigonometry Drill 1, Problem 1. What is the length of y?
ACT Math: Coordinate Geometry Drill 1, Problem 2. Solve the inequality and determine which solution is shown on the number line.
ACT Math 4.1 Elementary Algebra 266 Views
Share It!
Description:
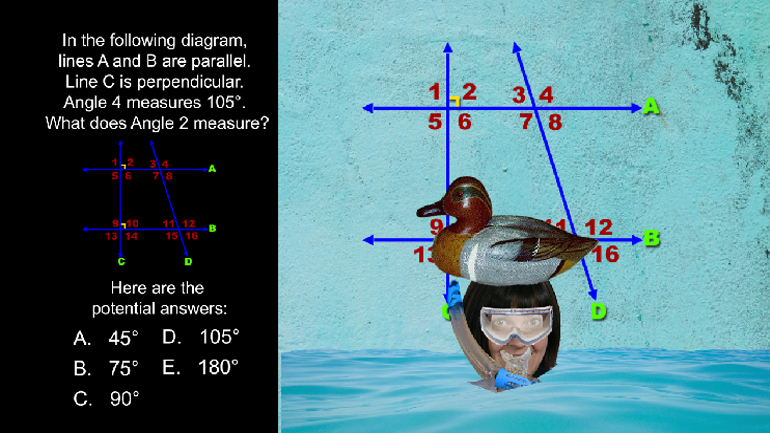
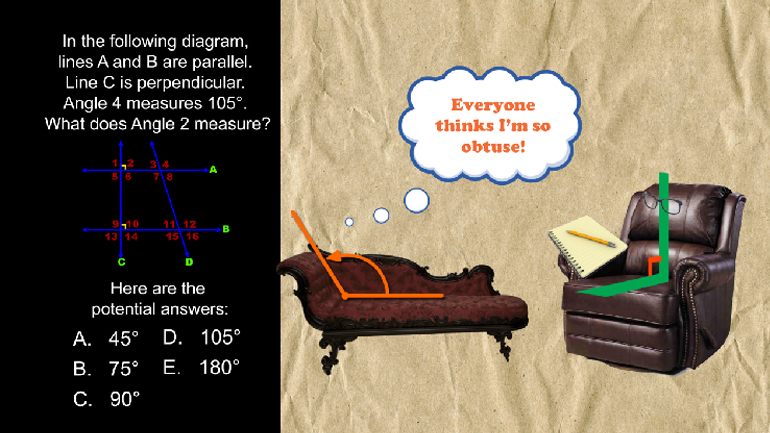
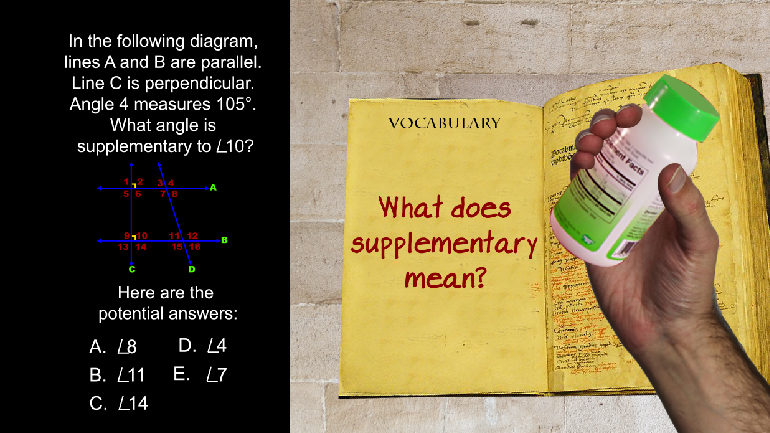
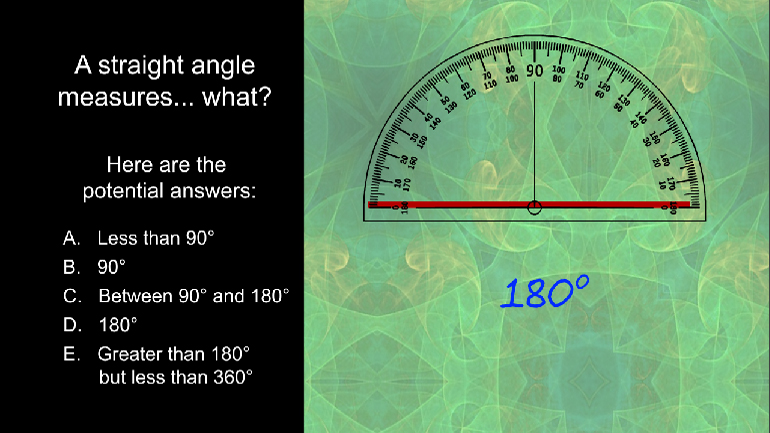
Elementary Algebra: Drill 4, Problem 1. Simplify the expression.
- Elementary Algebra / Applying properties of integer exponents and square roots
- Product Type / ACT Math
- Foreign Language / Spanish Subtitled
- Foreign Language / Korean Subtitled
- Foreign Language / Chinese Subtitled
- Foreign Language / Arabic Subtitled
- Number and Quantity / Extend the properties of exponents to rational exponents
- Number and Quantity / Extend the properties of exponents to rational exponents
- Elementary Algebra / Properties of exponents and roots
Transcript
- 00:03
And another Shmoop de jour for you and your.. brain.
- 00:06
Simplify: a to the 8 and one-half power.
- 00:10
And here are the potential answers...
- 00:14
Alright. Do we realize that when we raise an exponent to a power with a fraction...
- 00:18
...we can simply multiply those numbers together?
Full Transcript
- 00:22
In this case we are raising 'a' to the 8th power, which is then raised to the one-half power.
- 00:26
So we can do the dirty work first.
- 00:27
8 times 1/2 equals 4.
- 00:30
Which means we're left with a to the 4th power...and that's it.
- 00:33
Answer D.
Related Videos
ACT Math: Plane Geometry Drill 3, Problem 1. What is the area of the trapezoid shape in the video?
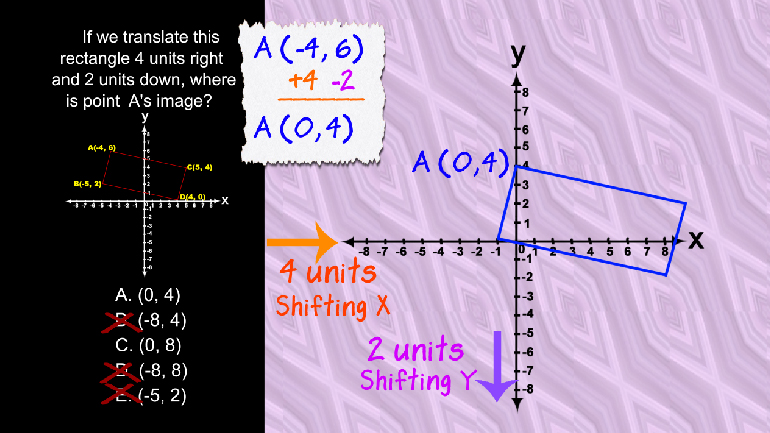
ACT Math: Coordinate Geometry Drill 1, Problem 1. Which inequality is expressed by the number line?
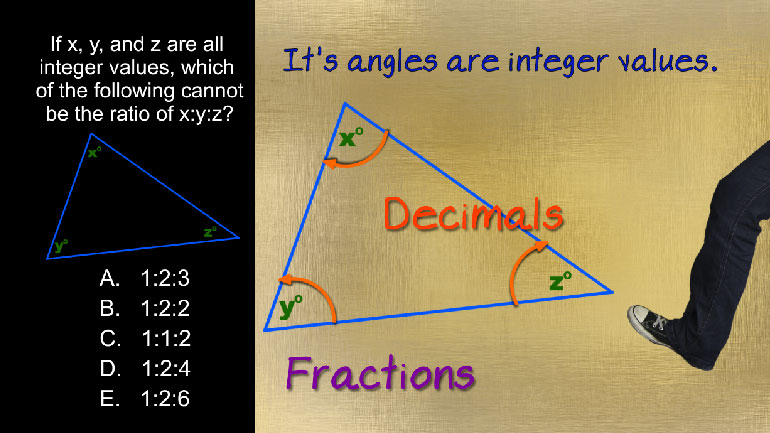
ACT Math: Intermediate Algebra: Drill 3, Problem 1. Find the fifth number in the series.
We don't like knocking people down to size, but we do like simplifying radicals. Join us?
If fleeing criminals always fled the scene of the crime at perfect right angles, it would be much easier to determine their whereabouts. Fortunatel...