7. Usa funciones inversas para resolver ecuaciones trigonométricas que surgen en contextos de modelos matemáticos; evalúa las soluciones empleando la tecnología y las interpreta en términos del contexto.

Los estudiantes deben saber que el hecho de que las funciones trigonométricas tienen que ver con los modelos, no significa que hagan pasarelas para las marcas Prada o Armani. Al menos, no desde que Secante se tropezó e hizo el ridículo en la pasarela de la Fashion Extravaganza de Milán en el 2007. La culpa fue de esos horribles tacones de aguja de 30 cm.

Las funciones trigonométricas prefieren otro tipo de modelaje. Estamos hablando de los triángulos, los osciladores armónicos y otros ámbitos de la geometría e incluso la física. Quizás no tengan tanto glamour, pero no dejan de ser muy importantes.

Los estudiantes deben poder aplicar las funciones de trigonometría y sus funciones inversas a situaciones específicas. En la mayoría de los casos, esto significa encontrar longitudes laterales, ángulos y proporciones de trigonometría de triángulos rectángulos. A veces, nuestro ángulo será θ. Otras será 2θ. ¿Pero qué si es θ² + 3θ – 40? Esto supone aplicar las funciones trigonométricas y usarlas de manera algebraica.

Como las ecuaciones trigonométricas pueden ser intimidantes, puede resultar útil resolver una ecuación trigonométrica y una ecuación regular de álgebra lado a lado mientras se compara cada paso. Los estudiantes verán que, del mismo modo que resuelven para x en una ecuación algebraica regular, deben resolver para θ en una ecuación trigonométrica.

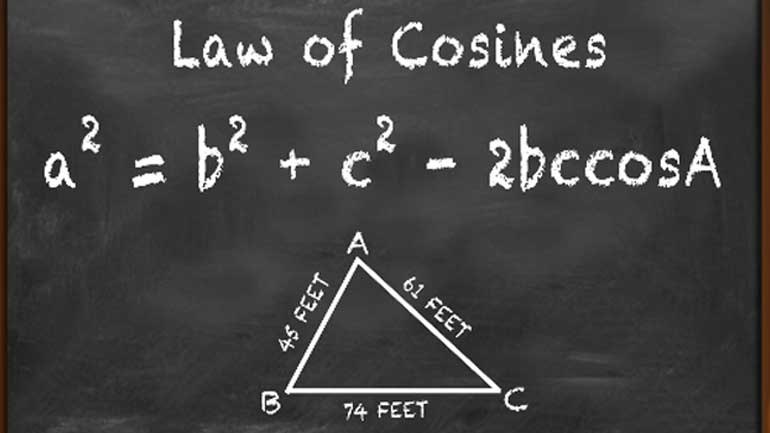
Una vez que se sientan cómodos con los ángulos rectángulos, pueden llevar las funciones trigonométricas al siguiente nivel. Podemos aplicar estas funciones para resolver triángulos que no sean triángulos rectángulos, empleando la Ley de Senos y la Ley de Cosenos.

Podemos usar funciones trigonométricas y sus funciones inversas para calcular elevaciones, evaluar distancias sobre cuerpos de agua, determinar ángulos para vehículos, calcular la longitud de onda de la luz, e incluso modelar nuestros ciclos de sueño. Es obvio que son útiles para más que saber acomodarse el sombrero Louis Vuitton en el ángulo perfecto (que es 19.4°, por si no lo sabías).

Este es un video que recapitula la Ley de Senos.

Asi como también recapitula la Ley de Cosenos.