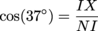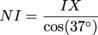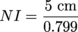First, we might want to draw a picture to make sense of everything that's going on here. 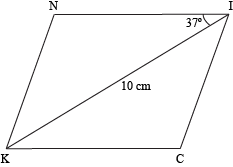
That's all the information we're given, but what else do we know about rhombi? We know they have perpendicular diagonals, so drawing in NC will make a 90° angle with KI. We also know that since a rhombus is a type of parallelogram, the diagonals bisect each other. Let's do that and see what we've got. 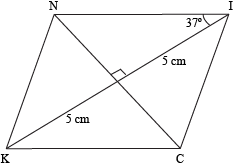
We're looking for the perimeter, and since the four sides are all congruent, all we need to do is find one of them and multiply it by 4. Oh, Geometry, thou art a sneaky subject! Of course, to find out information about quadrilaterals, we'll refer back to our good friends: triangles. Let's say point X is the spot where the two diagonals intersect. See the right triangle ΔNIX? If we sprinkle a little trigonometry into the mix, we'll have our perimeter in no time. The cosine corresponds to adjacent over hypotenuse, so the cosine of ∠NIX would be IX (the length of the adjacent side of the triangle) over NI (the length of the hypotenuse of the triangle). Since we know that m∠NIX = 37° and IX = 5 cm, we can find the length of NI. 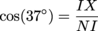
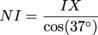
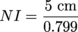
NI ≈ 6.26 cm Since NI is only one of the sides, we can multiply its length by 4 to get the perimeter of the rhombus. P = 4NI
P = 4(6.26 cm)
P = 25.04 cm |