Think you’ve got your head wrapped around Derivatives? Put your knowledge to
the test. Good luck — the Stickman is counting on you!
Q. f ' (x) =
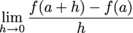
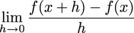
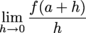
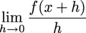
Q. Let f(x) = x2 – x. Calculate f ' (x).
f ' (x) = 2x + 1
f ' (x) = 2x – 1
f ' (x) = -2x – 1
f ' (x) = -2x + 1
Q. If f ' (x) = 4x2 + 3, find f ' (-2).
11
-19
19
There is insufficient information to answer this question.
Q. If f(x) is a line of the form f(x) = mx + b then
f ' (x) = m
f ' (x) = mx
f ' (x) = b
f ' (x) = 0
Q. A graph of the function f(x) is shown below.
The function f ' (x) is
always positive
always negative
positive when x is less than zero and negative when x is greater than zero.
negative when x is less than zero and positive when x is greater than zero.
Q. A graph of the function f(x) is shown below.
Insert Image DM-1
Which of the following could be the graph of f ' (x)?
Image DM-2
Image DM-3
Image DM-4
Image DM-5
Q. A graph of f ' (x) is shown below.
Image DM-6
Which of the following could be the graph of f(x)?
Image DM-7
Image DM-8
Image DM-9
Image DM-10
Q. If
- f is continuous on [a, b]
- f is differentiable on (a, b), and
- f(a) = f(b), then Rolle's Theorem tells us
the number of values c in (a, b) for which f ' (c) = 0.
that there is some c in (a, b) with f ' (c) = 0.
that there are infinitely many values of c in (a, b) with f ' (c) = 0.
the precise value(s) of c in (a, b) for which f ' (c) = 0.
Q. For which given function and interval are we allowed to use the Mean Value Theorem?
f(x) = |x| on (-1,1)
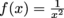on (0,2) f(x) = x2 – x on (-2, -1)
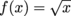on (-1, 1) Q. What does the Mean Value Theorem tell us about the function f(x) = x3 on the interval (-2,1)?
Nothing. We aren't allowed to use the Mean Value Theorem here.
There is some c in (-2,1) with f ' (c) = 0.
f ' (0) = 3.
There is some c in (-2, 1) with f ' (c) = 3.