The Durbin Watson Statistic lets us know when good statistical regression analysis has gone bad...like a donut that looks good on the outside, but is actually super stale. Nobody likes a stale donut.
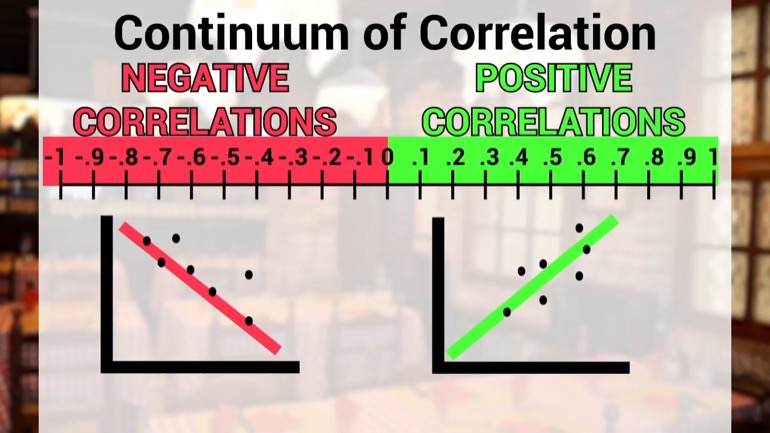
The Durbin Watson Statistic tests a time-series regression for autocorrelation, which we don’t want. Other tests might say “hey, you, your regression is looking good!” while the Durbin Watson Statistic test might say “uhmmm, actually, you should take another look...something’s not right, even if the others tests checked out.” The Durbin Watson Statistic gives a value of 2 if there’s not autocorrelation, or a value above or below 2 (within 0 - 4 range), which means there’s negative or positive autocorrelation.
So what is autocorrelation, and why is it bad? Regressions are functions that try to use a bunch of data to predict something. Basically, regressions are a statistical method to find correlations (it can’t prove causations, though...for that we’ve gotta have experiments) by fitting data to a line. Finding the best line for the data is the goal. How far the data points are from the line is the error, which we want to minimize to get the best fit line.
When there’s autocorrelation, that means your error value of your regression is correlated, either negatively or positively. If your regression “fits” the data well and your errors are correlated, that means something’s wrong. For instance, it could mean that you missed a really important variable that has some explanatory power, which shouldn’t be nested in your error, but a part of your regression line (omitted variable bias).
You can also get autocorrelation when your regression is functionally misspecified, which means your regression doesn’t actually fit the data well, because you have equal errors on both sides of your regression line, showing that you missed something in the relationship...which is kinda the point of doing a regression.
A third way you can get autocorrelation is measurement error in the independent variable, which will cause your independent variable and your error variable to both reflect that measurement error, and you’ll find your errors correlating over time with that measurement error.
Related or Semi-related Video

Finance: What is Inverse Correlation?1 Views
Finance Allah Shmoop What is inverse correlation All right It's
the relationship between two variables where we can expect an
increase in one variable to be paired with a decrease
in another variable Alright in plain English correlation When it
rains you get wet Inverse correlation When it rains you
get dry Correlation You have a big brain So your
smart inverse correlation like we're thinking dinosaurs Maybe they had
big brains all of it But if they had big
brains the bigger their brain Well the dumber thing God
Well that would be an inverse correlation right Correlation You
drive a fast flashy cars so you probably have a
small garage Alright Inverse correlation You drive a fast flashy
car and everything else about you is enormous Yeah So
in a word in versus just opposite check out inverse
correlations in this table showing to data sets Note how
the returns on investment in gold increase while the returns
on investment in Pat's for cats decrease over the same
timeframe And instead of hats for cats you could have
seen the stock market because people typically retreat into gold
when they're nervous about equities So this is really not
a bad inverse correlation right Okay So let's take a
look at a scatter plot of the same two data
sets See how the data points get lower and lower
as we go farther to the right Yeah that's because
the X values or the returns on the gold investment
increase or go farther to the right Well then the
Y values or returns on the hats for cats equities
investment decrease or go closer to the Y axis Well
sometimes we want to put a number on how strong
or weak The inverse correlation is between any two pairs
of variables So basically we're trying to determine if the
inverse correlation is one that follows a very steady amount
of decrease in one variable for a fixed amount of
increase in the other or if the amount of decrease
in one variable fluctuates for a fixed increase in the
other or more simply how closely the points on the
scatter plot are to an imaginary line like this thing
that best represents them Right That's an r squared correlation
there we'll get to it So the measure of how
strong the correlation is between these two variables is called
yes the correlation coefficient or our value Well a strong
inverse correlation would have the data points all cozied up
to the best fitting line coincidently called the line of
best fit Kind of like all of your new you
know friends after you win the ninety million dollars Powerball
lottery Well a week inverse correlation would have the data
spread out away from the line and best fit So
there's really no clustering here It's just a whole bunch
of dots on a graph that don't really tell you
much of anything you know like the location of kids
at a middle school dance compared to the location of
the dance floor So how do we find the our
value to determine how strong our correlation is inverse or
otherwise Well typically people use some sort of technological gadgets
such as a graphing calculator spreadsheet or a nap Let's
take that investment data from before comparing Gold returns to
returns on equity and hats for cats and walked through
how you'd find the R value using a spreadsheet So
open your favour like Excel or Google sheets or OpenOffice
Cal Core sells for days or and whatever you use
We're using Excel for this demo but they all work
in basically the same Put the data for the gold
returns without the presented signs in the first column Put
the data from hats for cats also without the presented
signs In the second column like that go to any
blank cell like the top selling the third column C
one there Then click on the formula's tab Choose the
Mohr Functions button and Anju Statistical See the coral option
there you selected Once we choose correlation we'll get a
pop up asking us to define the two sets of
data highlight on ly the first column of data It
should load that set of cells in the top row
of the pop up All right now left Click in
the second row of the pop up Highlight on ly
the second column of data and well should slide those
cells right into place Got it Okay So click okay
and boom instant our value Well it should show up
in the cell you picked to enter the Correlation Command
See one If you followed our Russians to et You
know t looks like our correlation has the strength of
negative point eight four Oh one Okay But like what
does that mean Is that strong or weak Positive Negative
Well for inverse correlations there's a range of values between
zero and negative one that we consider strong medium and
weak Inverse correlations like strong inverse correlation is generally run
from about negative point seven The negative one These will
be scatter plots where the points are quite close to
the best fit line like they're extremely counter or inversely
correlated Like if you found that every guy over forty
who drove a red convertible portion wore a gold chain
necklace there had a really big garage well then it
would be negatively correlated to our expectations Okay medium inverse
correlation is generally run from about negative point For the
negative point seven seas will be scattered plots with points
group less closely around the line A best fit Think
about it like well maybe half to two thirds of
all the guys have a small garage versus a big
garage Yeah something like that Weak inverse correlation is generally
run from well zero toe negative point for easily scatter
plots with almost no riel tight grouping Maybe there's some
trend if you really study it hard and think about
Roar Shack But there's really no correlation between the size
of your garage and when you're driving a convertible red
portion you wear a gold chain necklace All right one
thing we have to be careful about With the inverse
correlation XYZ thie implied value judgments that mistakenly get applied
to the two variables that are inversely correlated like in
our correlation calculation on returns we saw the gold investment
rise while the equity in hats for cats investment had
decreasing returns and basically was saying that people retreated putting
there cash into gold when they were nervous about the
equity markets Well that doesn't mean gold will always be
the one to increase While hats for cats decreases Beyond
the obvious changes in the market that might make gold
suddenly tank an inverse correlation means that gold could be
the investment with decreasing returns While hats for cat shows
increasing returns right the correlation thing is just showing that
they're inversely correlated When one goes up the other goes
down It could be that well when one goes down
the other one goes up Got it by the biggest
takeaway smelling That inverse correlation means that as one variable
increases in general the other variable decreases particularly when you
have high R squared correlations there Also we can calculate
how strong the correlation is by finding the R value
which we typically do using some technological do Dad Yeah
thank you Google Sheets and excel in all that stuff
Inverse correlation Czar values run from zero to negative one
with strong being in close to negative one in week
being close to zero And we're hoping there's an infamous
correlation between the number of matches we get on tinder
and the number of dates when we get that in
badly But well so far the data is not backing 00:06:41.135 --> [endTime] us up Change our picture what Oh
Up Next
What are correlation coefficients? Correlation coefficients are calculated variances between two variables within a given time period. As variable...